Research
Effect of Impacts on the Evolution of Planets
Modeling Techniques
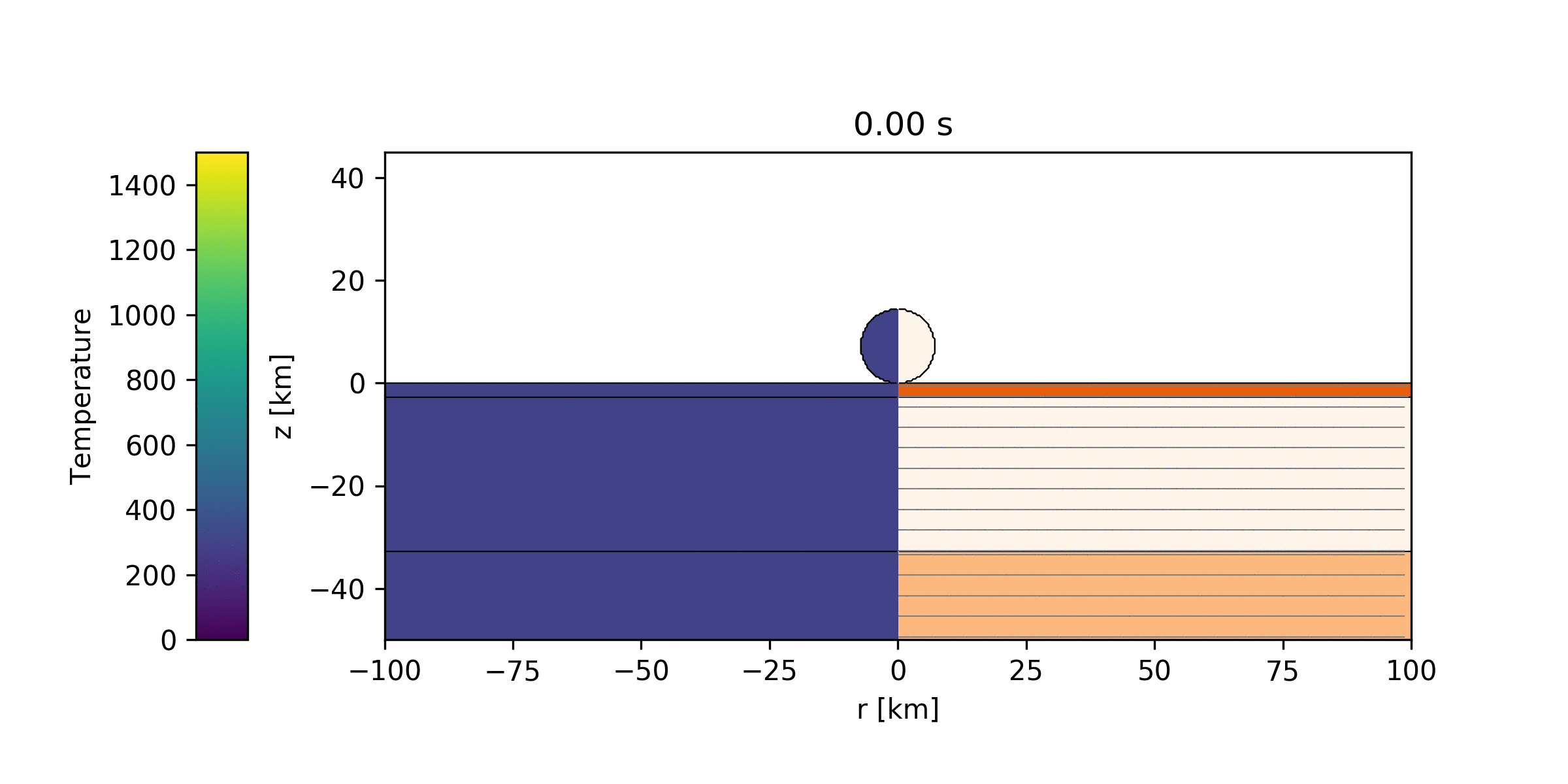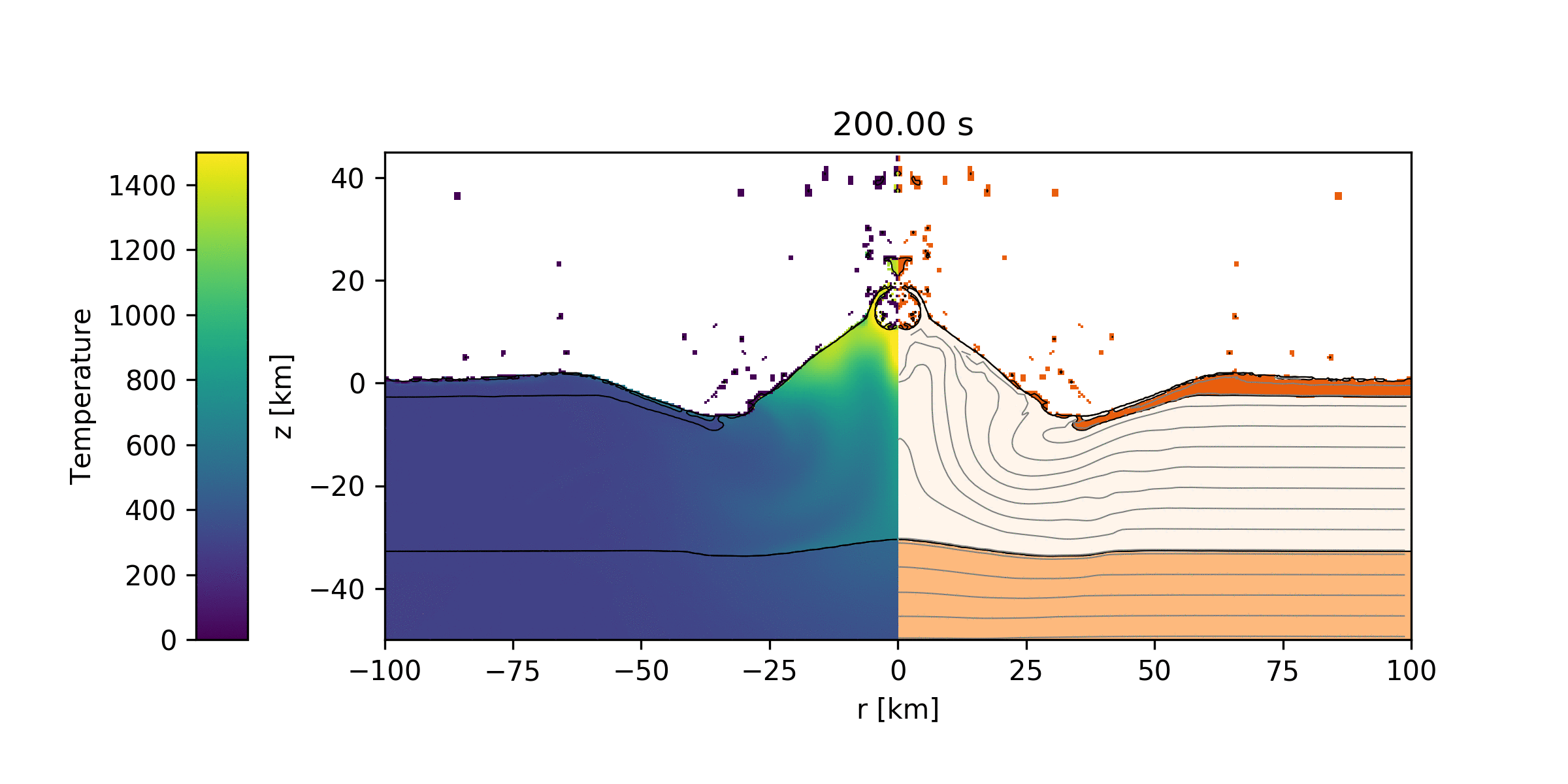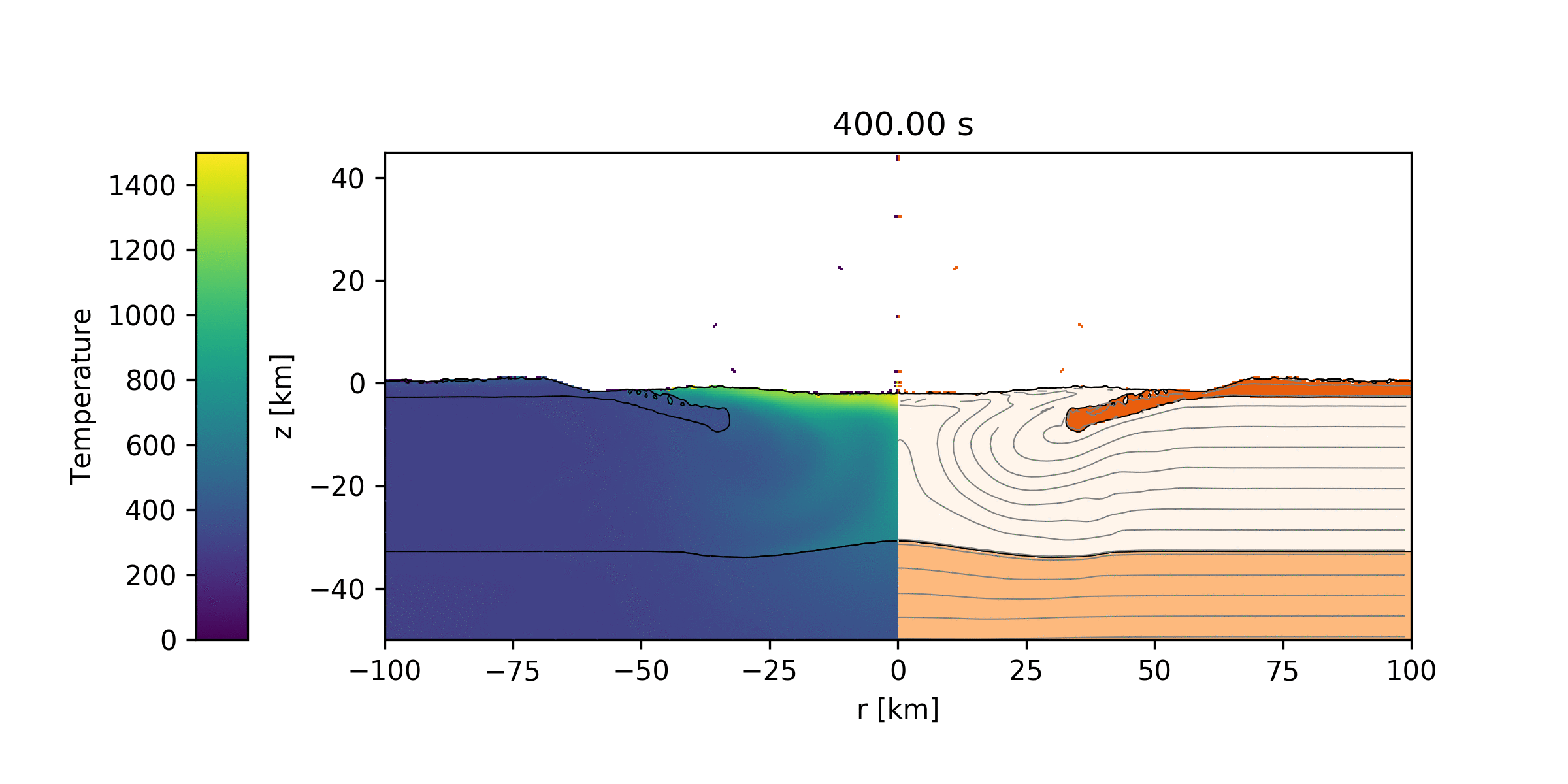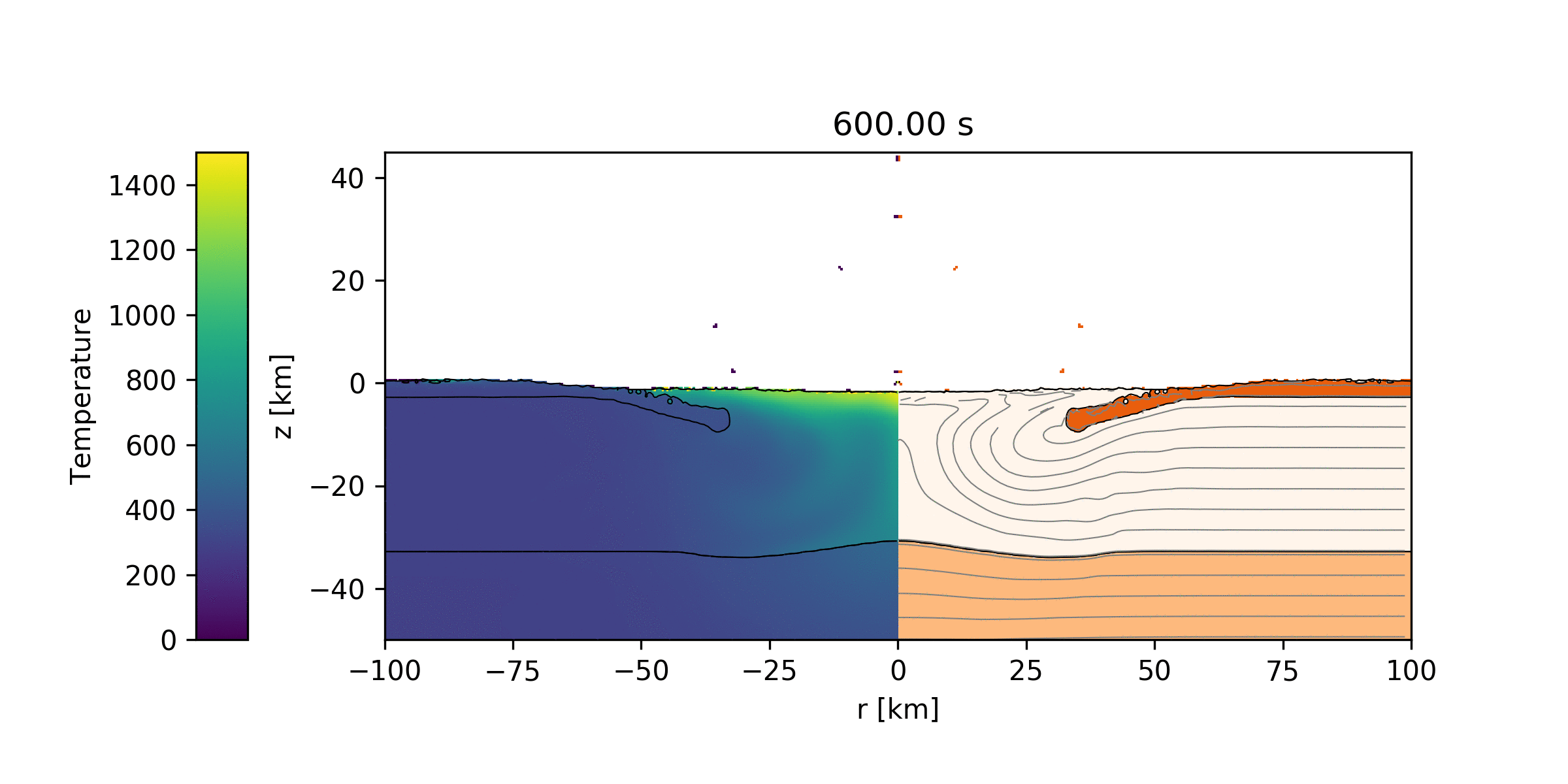
To model impacts, I use a physics code that has been developed by a number of people over many years called iSALE. This code uses a finite difference method to calculate how material behave under immense pressures and temperatures caused by impacts. Shown below are example simulations of the Chicxulub impact (one with a surface temperature of 300 K and the other with a surface temperature of 740 K).
Simulation of the Chicxulub impact where an impactor with a diameter of 14 km strikes the surface traveling at 12 km/s. Temperatures are shown on the left, while the three types of materials of the surface are shown on the right. The top (dark orange) layer is 3 km of sediment, the next (cream color) layer is the crust with a thickness of 30 km, and the bottom layer (light orange) is the mantle. The surface temperature is set to 300 K (Earth-like).
This simulation is the same as the previous one except that here the surface temperature is set to 740 K (Venus-like). Unlike the 300 K case where there was a bump in the mantle directly below the impact site, in the hotter temperature case the mantle is a lot flatter.
This plot shows the surface topography for the 300 K Chicxulub impact simulation. r is the horizontal distance from the center of the crater and z is the vertical distance.
Similar to the case with the bump in the mantle, notice how in this hotter case (740 K) the surface topography is flatter near the center of the crater? What this is showing is what we expect material to do. When material is hotter (even though we are talking about solid rock here), they tend to flow more easily than when they are colder.